BLANUŠIN GRAF
(I. Ivanšić)

 

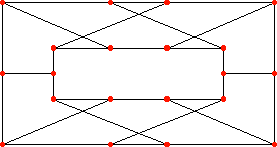
Sve češće srećemo termin Blanušin graf koji se nalazi u logotipu Hrvatskoga matematičkog društva (HMD), pa ga ovim prikazom želimo približiti našim čitateljima. Radi se o grafu na sl. 1., sa sljedećim svojstvom: iz svakog vrha izlaze po tri grane (trivalentni graf) čije je grane nemoguće obojiti s tri boje tako da iz svakog vrha izlaze sve tri boje. Tako ćemo za trivalentni graf govoriti da je "3-obojiv" ili da "nije 3-obojiv". 

 

                                  

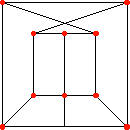 Slika 1.                                                           Slika 2.

 

Taj je graf otkrio profesor Danilo Blanuša (v. Glasnik matematički 22(42)(1987), 535-540) i objavio ga u svom radu [B] 1946. godine. Bio je to drugi poznati graf s navedenim  svojstvom. Prvi poznati prikazan je na sl. 2. i zove se Petersenov graf. Za njega je J. Petersen [P] dokazao da nije 3-obojiv. Sam je graf bio poznat i prije; vidi npr. [H-S] str. 124. U krugu matematičara koji su tada bili bliski takvim objektima i problematici vezanoj uz nju držalo se da je Petersenov graf jedini graf tog tipa, što se naravno nije uspijevalo dokazati. Nakon Blanušina otkrića nađen je već 1948.g. treći [D], 1973. g. četvrti [Sz], a 1975.g. našao je Isaacs [I] dvije beskonačne serije grafova sa spomenutim svojstvom. Otkrivač je trećeg grafa, objavljenog u [D], profesor W. T. Tutte koji je vidio Blanušin graf odmah nakon što je objavljen (podatak iz privatnog dopisivanja), a sam rad je objavljen pod pseudonimom. Kako je Blanušin rad objavljen na hrvatskome jeziku (sa sažetkom na francuskome), to je sretna okolnost da ga je odmah uočio W. T. Tutte. U [D] je na engleskome jeziku prezentirao i Blanušinu lemu o kojoj ćemo nešto reći kasnije. Blanušin graf je bio izložen na velikoj izložbi "Znanost u Hrvata, prirodoslovlje i njegova primjena", održanoj u Zagrebu (lipanj-listopad) 1996. godine i izložak je bio obojen s četiri boje.

Ovdje ćemo kratko prikazati što je Blanuša pisao u spomenutom radu, i što ga je navelo na otkriće tog grafa. U to je vrijeme bio dosta popularan tzv. "problem četiriju boja", koji se jednostavno i lako može formulirati ali se pokazao vrlo tvrdim problemom. Zamislimo na globusu (sferi) ili u ravnini nacrtanu zemljopisnu kartu kojom su sfera ili ravnina podijeljene u konačan broj povezanih područja. Tu kartu treba obojiti tako da područja sa zajedničkom granicom budu raznobojna. Pitanje je vrlo praktično: koliki je najmanji broj boja dostatan za bojenje svake karte pod spomenutim uvjetom? 

Istaknimo odmah da su razmatranja na sferi i u ravnini ravnopravna. Kada je karta u ravnini, tada "vanjski dio ravnine" moramo shvatiti kao područje. Imamo li kartu u ravnini, onda je stereografskom projekcijom prenesemo na sferu, a točku iz koje projiciramo priključimo području koje je okružuje. Gledamo li neku sfernu kartu, onda uočimo jedno područje na sferi i jednu njegovu unutarnju točku iz koje onda stereografskom projekcijom prenesemo kartu na ravninu. 

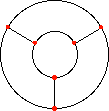
Lako se može vidjeti da tri boje nisu dostatne. Npr. kartu na sl. 3. ne možemo pod navedenim uvjetom obojiti s tri boje.

  

                                 

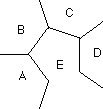Slika 3.                     Slika 4.a                     Slika 4.b

 

Kako je P. J. Heawood [H] naknadno dokazao da se svaka karta može obojiti s pet boja, problem bojenja sveo se na pitanje što je s četiri boje? A. B. Kempe [K] je 1879.g. publicirao rješenje koje je netočno, a tijekom godina napisano je i više knjiga na tu temu. Klasičnom se danas drži knjiga O. Orea [O]. 

Tri, četiri ili pet boja, kakvu to vezu ima s bojenjem trivalentnih grafova? Jasno je da su granice područja predstavljene ravninskim grafovima. Daljnje je pojednostavljenje problema četiriju boja u tome što je dovoljno promatrati karte koje imaju samo tromeđe. Navest ćemo kako se vidi da ne moramo promatrati četveromeđe, peteromeđe itd. Na sl. 4.a nacrtana je peteromeđa i crtkano jedan mali peterokut oko peteromeđe (vrha). Na sl. 4.b  obrisana je unutrašnjost peterokuta i jedna njegova stranica. Time smo dobili kartu koja ima samo tromeđe, a iz slike je jasno: ako se ta karta može obojiti s četiri boje, onda se i prije navedena karta može obojiti s četiri boje. To ćemo vidjeti  tako što ćemo "radijalno" stegnuti peterokut u vrh stare karte, a pri stezanju će nam vrhovi peterokuta opisati obrisane dijelove granice stare karte. Dakle, ako su četiri boje dostatne za karte s tromeđama, onda su dostatne za sve karte. Granice karata koje imaju samo tromeđe predstavljene su trivalentnim grafovima. Redukciju problema četiriju boja za opće planarne karte na karte koje imaju samo tromeđe dokazao je W. E. Story 1879.g. [S]. Granice tih karata su trivalentni grafovi koji se nalaze na sferi, odnosno u ravnini. Eto kako su se trivalentni grafovi pojavili u tom problemu. 

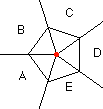
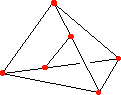
Istaknimo da postoje trivalentni grafovi koji se ne mogu nacrtati u ravnini ili na sferi kao što je ovaj na sl. 5. Taj graf predstavlja bridove tetraedra, pri čemu su spojena polovišta dvaju nasuprotnih bridova. Dakle, trivalentni grafovi koji se pojavljuju u ovoj problematici ravninski su ili sferni (mogu se smjestiti u ravninu ili sferu). Nadalje, u igri nisu niti svi ravninski trivalentni grafovi. U kartama obojenima pod uvjetom da su područja sa zajedničkom granicom raznobojna ne može se pojaviti npr. graf sa sl. 6., jer bi imao granicu g s čije bi obje strane karta bila obojena istom bojom. Osnovno je svojstvo grane g da se njezinim uklanjanjem graf raspada na dva dijela. Trivalentni grafovi bez takvih grana dobili su ime trivalentni grafovi bez "mostova". P. G. Tait [T] je 1880.g. dokazao da je problem četiriju boja za područja s tromeđama ekvivalentan problemu triju broja za trivalentne planarne grafove bez mostova. 

  

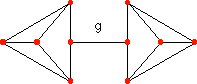                                          Slika 5.                                  Slika 6.

D. Blanuša je u svom radu predstavio dva rezultata. Prvo je tretirao upravo spomenutu ekvivalenciju dvaju problema i dao jedan svoj dokaz te ekvivalencije. Iako je time dao drukčiji dokaz poznate činjenice, taj se dokaz bazira na jednoj lemi koja je nova činjenica i lema se u [H-S] str. 82.-83. citira, dokazuje i komentira ovom rečenicom: "This will turn out to be very powerful lemma". (Pokazat će se da je to vrlo snažna lema). Dakle, pođimo od povezanog trivalentnog i 3-obojivog grafa. Presiječemo li neke grane postići ćemo da se u nekom koraku graf raspadne na dva dijela, tj. postane nepovezan. Nazovimo taj postupak "siječenje grana" (engl. edge cut). Kako je graf obojen, recimo crvenom, bijelom i plavom bojom, to neka smo u nekom siječenju presjekli c crvenih, b bijelih i p plavih grana. Blanušina lema kaže da su za svako siječenje grana brojevi c, b, p istog pariteta, tj. ili su sva tri parna, ili su sva tri neparna. 

Zatim se Blanuša osvrnuo na trivalentne grafove koji nisu 3-obojivi. Tako je primjerom pokazao (graf na sl. 1.) da postoje trivalentni grafovi koji nisu 3-obojivi, a kompliciraniji su od Petersenova što je u tom radu bilo stvarno otkriće. Blanušina je misao vodilja ciljala problemu četiriju boja, pa mislim da tada nije bio svjestan stvarnog otkrića. To se vidi iz posljednjeg ulomka rada [B] koji navodimo uz malo promijenjenu terminologiju. 

"Do sada su razni autori uglavnom istraživali samo ravninske trivalentne grafove bez mostova nastojeći dokazati da su 3-obojivi. Za neravninske trivalentne grafove su na temelju Petersenovog primjera znali da nisu svi 3-obojivi. No bilo bi zanimljivo istražiti i 3-neobojive trivalentne grafove. Kada bi uspjelo te grafove potpuno obuhvatiti i klasificirati, možda bi se dalo ustanoviti da li među njima ima ravninskih, pa bi onda tim putem bio riješen problem četiriju boja." 

Prema riječima Isaacsovim, 3-valentni grafovi koji nisu 3-obojivi rijetki su i teško ih je pronaći. U prilog tome najbolje nam govori ime koje im je 1976.g. dao M. Gardner [G]. On ih je nazvao snarks (tajanstvena nepostojeća bića), motiviran pjesmom "The Hunting of the Snark" Lewisa Carrolla. Taj su naziv  odmah prihvatili istraživači grafova, pa tako 3. poglavlje monografije [H-S] nosi naslov Snarks i u njemu su opisani i nacrtani The Blanuša Snarks. Od pojave tog naziva objavljeno je više radova u kojima se istražuju snarks. Blanuša je nadalje jednom rečenicom zabilježio da je graf dobio iz dvaju Petersenovih grafova "izbacivanjem dvaju čvorišta", u čemu je zapravo bila skrivena jedna operacija među grafovima. R. Isaacs je tu operaciju formalizirao i nazvao dot product te time generirao beskonačan niz trivalentnih grafova koji nisu 3-obojivi. U tom je smislu Blanušin graf B=P*P, gdje P označava Petersenov graf, B Blanušin graf a točka u sredini spomenutu operaciju dot product. Isaacs u [I] ističe da su njegovu konstrukciju inspirirali grafovi u [B], [D] i [Sz]. 

Problem je četiriju boja iritirajuće razumljiv svakome, pa je zato izazvao mnoge amatere, studente i profesionalne matematičare da o njemu razmišljaju. Jedno je jasno: samo njegovo rješenje nije promijenilo gotovo ništa u našem životu, ali je zadovoljilo ljudsku radoznalost i upornost. S druge je strane bio izvor istraživanja koja su dala vrlo značajna različita otkrića i rezultate, naročito u teoriji grafova. Tako je bilo i s Blanušinim radom [B] u kojemu nije riješen taj problem, ali su u njemu svi novi rezultati od trajne vrijednosti. 

U ožujku 1996. je Skupština Hrvatskoga matematičkog društva odlučila da Blanušin graf bude sastavni dio logotipa Društva. Gospodin Nenad Dogan je to realizirao onako kako to prikazuje sljedeća slika (sl. 7).

  

 Slika 7.

Mislim da imamo jedan od najljepših i najmodernijih logotipa matematičkih strukovnih udruga.

  

 Bilješka iz povijesti problema četiriju boja.

Problem je najmanjeg dostatnog broja boja za bojenje karata prirodan i vjerojatno se nikada neće pronaći ime čovjeka koji ga je prvi formulirao. No kako je problem postajao sve vrući, pojedini su ljudi pokušali naći njegov izvor. Ta su istraživanja pronašla pisani trag koji počinje s 23. listopadom 1852.g. To je nadnevak pisma A. de Morgana prijatelju i profesoru W. R. Hamiltonu u kojemu između ostalog u prijevodu piše kako ga je jedan njegov student pitao da mu opravda činjenicu, za koju ne znam je li činjenica ili nije, a to je da su četiri boje dostatne za bojenje bilo koje karte. Uz određeni komentar A. de Morgan dalje pita Hamiltona može li se dokazati da je nužno pet boja. U [F] je objavljena fotokopija toga pisma. Sljedeći je pisani trag mlađi tridesetak godina, a nadnevak mu je 13. lipnja 1878., kada je A. Cayley, na sastanku Londonskog matematičkog društva [C] ponovno postavio isti problem. Ubrzo nakon toga objavljena su dva neispravna dokaza; jedan je objavio P. G. Tait, a drugi A. B. Kempe. Na neispravnost je Taitova rješenja ukazao J. Petersen [P] demonstriravši da graf s sl. 2. nije 3-obojiv. Na neispravnost Kempeova rješenja ukazao je P. J. Heawood [H] koji se ujedno poslužio tim rješenjem kako bi dokazao da je pet boja dostatno. Zna se ime tog studenta; bio je to fizičar Frederick Guthrie, međutim, on je A. de Morganu prenio tvrdnju svog brata, matematičara Francisa Guthrieja, koji o tome nije nikada ništa publicirao. U nepisanom dijelu drži se da je problem bio poznat L. Euleru i A. F. Möbiusu, a vjerojatno i ponekome još. Problem su 1977.g. riješili K. Appel i W. Haken. U [A-H-1] dali su lijep povijesni prikaz problema, ali i pregledni prikaz njihova rada u kome su se služili kompjutorima. Sâmo je rješenje publicirano u [A-H-2] i [A-H-K] i zapravo predstavlja popravak Kempeova rješenja [K]. 

Napomena: godine navedene u tekstu godine su pripadajućih publikacija u kojima su objavljene.

Biografska bilješka.

Danilo BLANUŠA (Osijek, 07. prosinca 1903. - Zagreb, 08. kolovoza 1987.), matematičar, fizičar i inženjer. Osnovnu je školu pohađao u Beču i Steyr-u (Gornja Austrija), gimnaziju u Zagrebu i Osijeku. Studirao je elektrotehniku na Tehničkim visokim školama u Zagrebu i Beču. U Beču je paralelno bio izvanredni student Filozofskog fakulteta i studirao matematiku i fiziku. Radnu je karijeru započeo u Gradskoj električnoj centrali u Zagrebu. Nakon obrane doktorske disertacije čistog matematičkog sadržaja i habilitacije, imenovan je za izvanrednog profesora Tehničkog fakulteta u Zagrebu. Predavao je matematičke predmete na Tehničkom, Prirodoslovno-matematičkom i Elektrotehničkom fakultetu u Zagrebu. Od 1952.g. je izvanredni, a od 1958. g. redovni član Jugoslavenske akademije znanosti i umjetnosti u Zagrebu (danas HAZU). Bio je dopisni član Austrijske akademije znanosti i Srpske akademije nauka i umetnosti. Dobitnik je nagrade Ruđer Bošković za 1960.g.; nagrade grada Zagreba za 1967.g.; nagrade za životno djelo za 1974.g. Bio je odlikovan ordenom rada s crvenom zvijezdom i ordenom za narod za zlatnom zvijezdom. Postigao je u svijetu zapažene rezultate u različitim područjima znanstvenog rada. U matematici je postigao značajne rezultate u teoriji specijalnih funkcija (Besselove funkcije), u diferencijalnoj geometriji (izometrička smještanja hiperboličkih prostora u euklidske), u teoriji grafova (Blanušin graf), dok su radovi iz fizike vezani za teoriju relativnosti, a posebno fenomenološku termodinamiku.

 

Bibliografija.

[A-H-1] K. Appel and W. Haken, The Solution of the Four-Color-Map Problem, Scientific American 237(4)(1977), 108-121.

[A-H-2] ____________, Every planar map is four colorable. Part I: Discharging, Illionis J.Math. 21(3)(1977), 429-490.

[A-H-K] K. Appel, W. Haken and J. Koch, Every planar map is four colorable. Part II: Reducibility, Illionis J. Math. 21(3)(1977), 491-567.

[B] D. Blanuša, Problem četiriju boja, Glasnik Mat.-Fiz. Astr. Ser.II. 1(1946), 31-42.

[C] A. Cayley, On the colouring of maps, Proc. London Math. Soc. (1878), 148; Proc. Roy. Geographical Soc. 1(1879), 259.

[D] B. Descartes, Network-colourings, Math. Gazette, London 32(1948), 67-69.

[F] R. und G. Fritsch, Der Vierfarbensatz Geschichte, topologische Grundlagen und Beweisidee, Bibliographisches Institut - Wissenschaftsverlag, Manhaim 1994.

[G] M. Gardner, Snarks, Boojums and other conjectures related to the four-color-map theorem, Scientific American 234(No 4)(1976), 126-130.

[H] P. J. Heawood, Map-colour theorems, Quart. J. Math. Oxford 24(1890), 332-338.

[H-S] D. A. Holton and J. Sheehan, The Petersen Graph, Australian Mathematical Lecture Series 7, Cambridge Univ. Press, Cambridge 1993.

[I] R. Isaacs, Infinite families of nontrivial trivalent graphs which are not Tait colorable, Amer. Math. Monthly 82(1975), 221-239.

[K] A. B. Kempe, On the geographical problem of the four colors, Amer. J. Math. 2(1879), 193-200.

[O] O. Ore, The Four Color Problem, Academic Press, New York, 1967.

[P] J. Petersen, Sur le théoreme de Tait, L'Intermédiare des Mathématiciens 5(1898), 225-227.

[S] W. E. Story, Note on Mr. Kempe's paper on the geographical problem of the four colours, Amer. J. Math. 2(1879), 201-204.

[Sz] G. Szekeres, Polyhedral decompositions of cubic graphs, Bull. Austral. Math. Soc. 8(1973), 367-387.

[T] P. G. Tait, Remarks on the colouring of maps, Proc. Ray. Soc. Edinburgh 10(1880), 729.